Cuando se trata de resolver ecuaciones matemáticas en Linux, hemos discutido anteriormente GeoGebra, un software para geometría y gráficos 2D. Sin embargo, si está buscando herramientas más potentes, debería probar Sage. Todos hemos oído hablar de Matlab o Magma, pero Sage ofrece una alternativa de código abierto a esos dos y, en mi opinión, es más fácil de usar.
Instalación
Sage siempre está bajo un intenso desarrollo, lo que significa que se agregan nuevas mejoras con mucha frecuencia. Para instalarlo desde la fuente:
Primero, deberá satisfacer algunas dependencias.
sudo apt-get install build-essential m4 gfortran libssl-dev dpkg-dev
A continuación, puede descargar las fuentes desde el Página Oficial. Extráigalos y desde una terminal, inicie el script.
Nota: Necesitará alrededor de 3 GB de espacio libre para que Sage funcione correctamente. Asegúrese de tenerlos antes de iniciar la compilación (que llevará algún tiempo).
Si prefiere la versión binaria, también hay un PPA disponible para Ubuntu:
sudo apt-add-repository -y ppa:aims/sagemath sudo apt-get update sudo apt-get install sagemath-upstream-binary
También puede instalar todos los paquetes opcionales:
sudo apt-get install texlive evince xpdf xdvi tk8.5-dev
Uso
Para iniciar Sage, puedes hacerlo con el comando
del directorio descargado.
Si desea iniciar sage desde cualquier lugar, puede crear un enlace simbólico con
ln -s [path to the sage launcher] /usr/local/bin/sage
o incluso crea un alias en tu archivo ~/.bashrc como hice yo:
alias sage=/home/adrien/sage-5.2/sage
Sage es una herramienta no gráfica por defecto. En el lanzamiento, debería obtener algo como esto
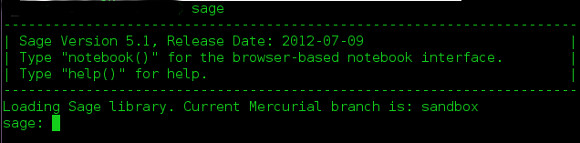
Luego tiene la opción: continuar con la consola o ir a la GUI basada en navegador escribiendo
Ambos son bastante equivalentes en términos de funcionalidad. La GUI es más intuitiva, especialmente para diagramas y gráficos, pero la terminal también funciona bastante bien. Con la GUI, pruebe el comando
circle((0,0), 1, rgbcolor=(1,1,0))
Verás un círculo amarillo debajo de él.
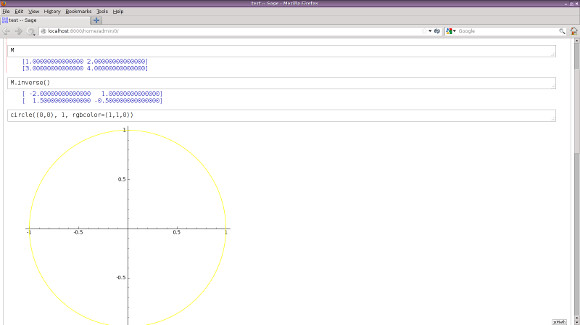
Si hace lo mismo en la consola, su visor de imágenes predeterminado se abrirá y mostrará el mismo círculo.
Nota: Tanto la GUI como la consola tienen una función de finalización automática.
Ahora que ha elegido la interfaz de Sage, podemos comenzar a hablar sobre las funciones en sí. Sage es absolutamente enorme, y lo digo en serio. Simplemente no hay forma de que podamos discutir todos los aspectos en un artículo. En su lugar, le mostraré algunas aplicaciones comunes que tal vez quiera probar.
1. Calculadora
Sí, Sage puede hacer algunas operaciones matemáticas básicas. Suma, multiplicación, etc. Dado que está escrito principalmente en Python, también puede usar la sintaxis de Python para hacer cosas como la división de enteros.
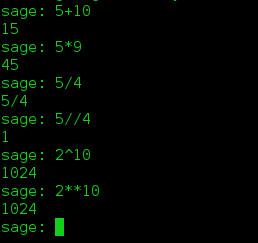
2. Raíces de polinomios
Es bastante común que te den un polinomio y que te pregunten por sus raíces. Con Sage, primero creas un anillo polinomial con
P.<x> = PolynomialRing(RR)
donde x será el generador y RR los números reales. Si desea que su anillo esté sobre los números racionales, por ejemplo, reemplace RR por QQ. Luego copia su polinomio:
Y luego pides las raíces.
Nota: esto devolverá las raíces en el anillo base del polinomio y sus multiplicidades. Si quiere que las raíces sean de otro anillo base, póngalo como argumento para la función roots().
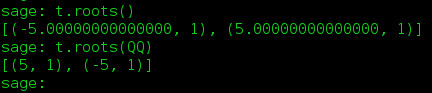
3. Matriz inversa
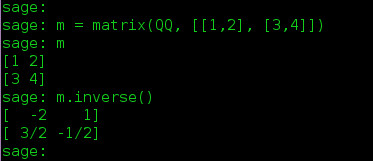
Si te gusta el comercio o la economía, es posible que hayas visto matrices en algún momento de tu vida. Generalmente, existe todo un proceso para encontrar las inversas de estas matrices. Bueno, Sage lo hace por ti de manera muy simple. Crea tu matriz sobre el anillo base que quieras.
m = matrix(QQ, [[1, 2], [3, 4]])
Y para buscar su inversa:
4. Gráficos
Sage también tiene algunas capacidades gráficas. Antes dibujamos un círculo con
circle((0,0), 1, rgbcolor=(1,1,0))
Estoy bastante seguro de que entendiste que el primer parámetro era el centro del círculo, el segundo era el radio y el último era el color del círculo en el estándar RGB. Bueno, también puedes trazar funciones básicas declarando primero una variable:
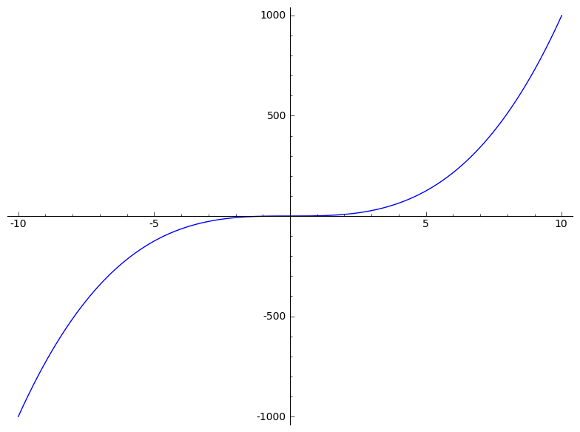
Y luego usa la función plot():
El primer argumento es la ecuación de la función, el segundo es el lapso. Así que aquí estaba preguntando por la función cúbica que se muestra de -10 a 10 en el gráfico x.
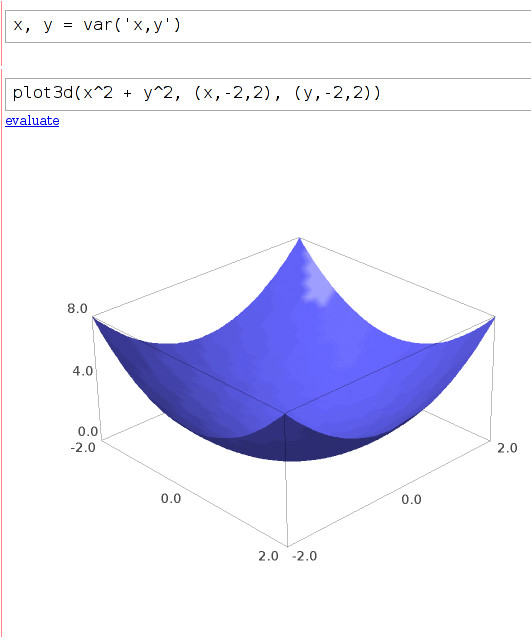
Nota: Si tiene instalado Jmol, puede incluso hacer gráficos en 3D declarando dos variables
Y luego usa la función plot3d():
plot3d(x^2 + y^2, (x,-2,2), (y,-2,2))
5. Resolución de ecuaciones
A veces queremos una solución para una ecuación, pero la calculadora solo nos da una aproximación. Es aún peor si hay algunas otras variables en esa ecuación y queremos que la solución se exprese en función de ellas. Durante años en la escuela secundaria, estuve atascado haciendo eso manualmente. ¡Que tonto! Sage lo hace a la perfección. Declara todas tus variables
x, a, b, c = var('x a b c')
Y luego simplemente use la función solve(), con la(s) ecuación(es) como primer argumento, y la(s) variable(s) que desea que se expresen después:
solve([x - 3*a == 6, x + b*c == 10], x, b)
Desearía haberlo sabido en la escuela secundaria…

6. Diferenciación e Integración
Aquí está la aplicación definitiva cuando eres realmente perezoso. Puede utilizar este programa para diferenciar e integrar funciones. Como de costumbre, declara tus variables
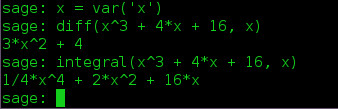
Y luego use la función diff() o integrate().
para diferenciar y
integral(x^3 + 4*x + 16, x)
por integrar.
Conclusión
Sage es realmente una herramienta increíble. La sintaxis se aprende rápidamente y se mantiene bastante estándar. El inconveniente es que la documentación es realmente algo que debe leer para comprender lo que realmente puede hacer. Las aplicaciones son tantas que es fácil perderse. Puedes hacer ecuaciones diferenciales junto con criptografía. Y se vuelve tan específico que en este momento se está desarrollando una función para encontrar el campo de división de polinomios sobre un campo finito (sí, tampoco tengo idea de lo que significa).
¿Tienes algún otro ejemplo que proponer? ¿Una pregunta sobre Sage? Por favor, háganos saber en los comentarios.
Credito de imagen: Matemáticas de Big Stock Photo.
